理解纳维尔，斯托克斯方程前言纳维尔，斯托克斯方程是描述流体的运动和行为的基本方程之一，它是一个偏微分方程组，用于计算流体的速度、压力和温度等物理量，纳维尔，斯托克斯方程纳维尔，斯托克斯方程可以写成以下形式，ρ，∂u，∂t，u·∇u，=，∇p，μ∇²u，λ，μ，∇，∇·u，其中，ρ是流体的密度u是流体的速度矢量t是时间p是流体的压力μ...。

引言纳维尔，斯托克斯方程是流体力学中的基本方程之一，它描述了流体的运动状态，对于非专业人士来说，理解纳维尔，斯托克斯方程可能会有一些困难，本文将从基础出发，一步步解析纳维尔，斯托克斯方程，并利用张量语言对其进行简化，让读者能够更深入地理解流体力学中的基本原理，矢量微积分与微分几何在学习纳维尔，斯托克斯方程之前，我们需要先了解矢量微积分...。

纳维尔，斯托克斯方程是描述流体运动的核心方程，但它的表述形式复杂，难以理解，通过张量语言的简化，我们可以更透彻地理解其内涵，与牛顿运动定律的联系纳维尔，斯托克斯方程实质上是牛顿第三定律在流体中的表达，牛顿第三定律指出，作用力与反作用力在大小上相等、方向相反，在流体中，作用力表现在两种形式，压力梯度项和粘滞项，压力梯度项描述流体内部压力...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组微分方程，描述了流体的运动，它们由克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯于19世纪初独立提出，方程描述纳维尔，斯托克斯方程描述了流体中任一点的速度、压力和应力的关系，它们由以下公式表示，ρ，∂u，∂t，u·∇u，=，∇p，μ∇2u，ρg其中，ρ是流体的密度u是流体的速度p是流...。

理解纳维尔，斯托克斯方程，张量语言的简化1.纳维尔，斯托克斯方程的本质纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体运动的方程，它是一个矢量微分方程，涉及流体的速度、压力、粘度和密度，方程的形式为，ρ，∂v，∂t，=，∇p，μ∇^2v，ρg其中，ρ是流体的密度v是流体的速度p是流体的压力μ是流体的粘度g是重力加速度2.与牛顿运...。

纳维尔，斯托克斯方程在流体力学中具有重要意义，它描述了流体的运动行为，理解该方程并非易事，本篇文章将利用张量语言，帮助读者简化流体力学中的矢量计算，并深入理解纳维尔，斯托克斯方程与牛顿运动定律之间的关联，矢量微积分与微分几何传统的流体力学依赖于矢量微积分，其运算依赖于大量的公式和技巧，相比之下，张量语言作为一种高级数学工具，可以极大地...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组非线性的微分方程，描述了流体的运动，它由法国工程师克劳德，路易·纳维和爱尔兰数学家乔治·加布里埃尔·斯托克斯于19世纪提出，纳维尔，斯托克斯方程与牛顿运动定律的关系纳维尔，斯托克斯方程可以看作是牛顿第二运动定律在流体中的应用，牛顿第二运动定律指出，物体的加速度与其质量和作用于物体的合力...。

引言纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它以数学的形式表达了流体在受力作用下的运动规律，本文将探讨纳维尔，斯托克斯方程的理解方式，及其与牛顿运动定律之间的关联，张量语言在流体力学中的应用张量语言是一种数学语言，可以用来简洁地描述具有多重分量的物理量，在流体力学中，利用张量语言可以大幅简化矢量计算，减少技术细节的干扰...。

纳维尔，斯托克斯方程是流体力学中的一个方程组，描述了流体的运动，该方程组可以通过张量语言来简化，这是一个强大的数学工具，可以在矢量微积分中使用，纳维尔，斯托克斯方程纳维尔，斯托克斯方程可以表示为，$$\rho\frac，\partial\mathbf，v，\partialt，\rho，\mathbf，v，\cdot\nabla，...。

引言纳维尔，斯托克斯方程是一组偏微分方程，描述了不可压缩、粘性流体的运动，它是流体力学的基础，在工程、气象学和其他领域有广泛的应用，纳维尔，斯托克斯方程以其复杂性和难以求解而闻名，本篇文章将深入解析纳维尔，斯托克斯方程，探索它与牛顿运动定律之间的联系，以及如何利用张量语言简化流体力学中的矢量计算，张量语言在流体力学中的应用张量语言是一...。

纳维尔，斯托克斯方程是一组偏微分方程，描述了粘性流体的运动，它们是流体力学中的基本方程，广泛用于建模液体和气体的流动，例如水流、空气流和血液流动，与牛顿运动定律的关联纳维尔，斯托克斯方程是牛顿运动定律在流体中的应用，牛顿第二运动定律指出，作用在物体上的合力等于其质量乘以加速度，纳维尔，斯托克斯方程提供了流体微元的合力的具体表达式，从而...。

纳维尔，斯托克斯方程，理解与应用导言纳维尔，斯托克斯方程是流体力学中的基本方程之一，描述了流体运动的数学模型，它通过将流体视为连续介质，即可以被无限细分而不会改变其性质，来表述其运动状态，本文将从张量语言的角度阐述纳维尔，斯托克斯方程，并探讨其与牛顿运动定律之间的关联，纳维尔，斯托克斯方程在张量标示法中，纳维尔，斯托克斯方程可以表示为...。

纳维尔，斯托克斯方程，使用张量语言简化流体力学纳维尔，斯托克斯方程是什么，纳维尔，斯托克斯方程是一组非线性偏微分方程，描述了流体的运动，这些方程以19世纪物理学家纳维尔和斯托克斯的名字命名，纳维尔，斯托克斯方程用于对不可压缩牛顿流体的流动进行建模，它们等效于牛顿第三定律，作用力等于反作用力，在流体中的表达，牛顿运动定律与纳维尔，斯托克...。

纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组非线性偏微分方程，用于描述流体的运动，它由法国数学家克洛德，路易·纳维和爱尔兰物理学家乔治·加布里埃尔·斯托克斯于19世纪提出，纳维尔，斯托克斯方程可以描述各种流体，从可压缩气体到不可压缩液体，它们用于模拟天气预报、飞机设计和生物医学等领域中的流体行为，纳维尔，斯托克斯方程与牛顿运动定律纳...。

引言纳维尔，斯托克斯方程是流体力学中最重要的方程之一，描述了流体的运动，要了解这个方程，我们需要先了解张量语言，张量语言张量是数学中描述多维空间中量的一种工具，一阶张量就是矢量，二阶张量是矩阵，张量语言的好处是可以简化流体力学中的矢量计算，矢量微积分与张量语言矢量微积分是传统的流体力学工具，但张量语言可以简化其运算，例如，点乘可以用张...。

导言纳维尔，斯托克斯方程是描述流体运动的基本方程组，它以爱尔兰科学家乔治·加布里埃尔·斯托克斯爵士和法国数学家克劳德，路易·纳维的名字命名，是流体力学的基础，张量语言的简化力量传统的流体力学计算涉及大量的矢量计算，这些计算既复杂又容易出错，张量语言是一种强大的数学工具，它可以显著简化这些矢量计算，张量是具有多个分量的数学对象，它们可以...。

纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组微分方程，用于描述流体力学中流体的运动，它们以方程组的形式表达了牛顿第三运动定律，作用力等于反作用力，在流体中的应用，纳维尔，斯托克斯方程可以写成以下形式，$$\rho\frac，D\mathbf，u，Dt，=，\nablap，\mu\nabla^2\mathbf，u，$$其中，$\r...。

纳维尔，斯托克斯方程是流体力学中用来描述流体运动的基本方程，它以法国工程师克劳德，路易·纳维尔和爱尔兰数学家乔治·加布里埃尔·斯托克斯的名字命名，该方程是一个非线性偏微分方程组，用于描述流体的速度、压力和密度等物理量随时间和空间的变化，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程可以看作是牛顿运动定律在流体中的表达，牛顿运动...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它是一个非线性偏微分方程组，如何理解这个方程组的物理意义，并将其与牛顿运动定律联系起来，是流体力学研究中的一个重要课题，张量语言在流体力学中的应用张量语言是一种数学工具，可以简化矢量微积分中的计算，在流体力学中，张量语言可以用来描述流体的运动、应力和应变，利用张量语言，我们可以将...。

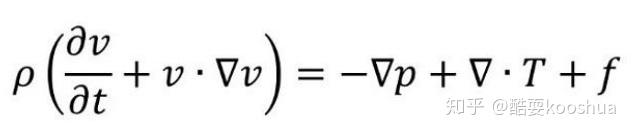
如何理解纳维尔，斯托克斯方程张量语言简介在流体力学中，矢量计算往往复杂繁琐，张量语言是一种简洁而有力的数学工具，可以极大地简化这些计算，在张量语言中，矢量被视为一阶张量，二阶张量则需要两个基底的张量积来展开，点乘和叉乘的张量表示矢量的点乘和叉乘可以通过张量进行表示，点乘，两个一阶矢量的缩并叉乘，一个一阶矢量与一个二阶张量的点乘，结果为...。

纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它是一个偏微分方程组，很难解析求解，张量语言的简化张量是描述物理量的数学工具，用张量语言可以简化流体力学中的矢量计算，使其更易于理解和推导，一阶和二阶张量矢量可以表示为一阶张量，用基底写成逆变形式，$$v^\alpha=，v^1，v^2，v^3，$$二阶张量需要用两个基底的...。

前言在流体力学中，纳维尔，斯托克斯方程是一组复杂的偏微分方程，描述流体的运动，它以克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯的名字命名，他们于19世纪制定了该方程，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程是牛顿第三运动定律在流体中的表达方式，它表示流体微元的受力等于作用在它上面的压力梯度和粘滞力，纳维尔，斯托克斯方...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程组，它是一个偏微分方程，将流体的质量、动量和能量联系起来，牛顿运动定律与纳维尔，斯托克斯方程的关联纳维尔，斯托克斯方程实际上是牛顿运动定律在流体中的表现形式，牛顿第三定律指出，作用力和反作用力大小相等，方向相反，这在流体力学中表现为，压强梯度力，流体中的压强...。

导言纳维尔，斯托克斯方程是描述流体运动的基本方程，它以数学形式表达了牛顿第二运动定律在流体中的应用，张量语言的引入张量语言是一种数学工具，可以简化流体动力学中的矢量计算，它允许我们用一个统一的符号表示点乘、叉乘和导数等运算，一阶张量又称矢量，可以用逆变形式表示为$V^，\alpha，$，其中$\alpha=1，2，3$是三个空间分量，...。

纳维尔，斯托克斯方程是流体力学中的基础方程，描述了流体的运动，它与牛顿运动定律有着密切的关系，可以通过牛顿第三定律导出，在传统的流体力学教材中，纳维尔，斯托克斯方程往往用矢量微积分的形式表示，这使得计算过程繁琐复杂，如果采用张量语言，纳维尔，斯托克斯方程的表达就会大大简化，张量语言是一种数学工具，它可以将矢量和二阶张量等物理量表示为坐...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程纳维尔，斯托克斯方程是流体动力学中的一组偏微分方程，描述了流体的运动，它由克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯于19世纪开发，方程组如下，ρ，∂u，∂t，ρ，u·∇，u=，∇p，μ∇²u，μ，4，3，η，∇，∇·u，其中，ρ是流体的密度u是流体的速度p是流体中的压强μ是流体...。

2023年10月27日12时，，张朝阳的物理课，第二百二十八期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，首先回顾了如何用张量形式表达矢量微积分中的相关计算，再利用张量分析的方法从流体应力张量中导出了流体微元的受力，纳维尔，斯托克斯方程及其与牛顿运动定律的关联纳维尔，斯托克斯方程是流体力学中的基本方程之一...。

引言纳维尔，斯托克斯方程是描述流体运动的数学方程组，对于了解流体力学至关重要，这些方程的复杂性可能令人望而生畏，本文将通过张量语言，简化流体力学中的矢量计算，从而帮助理解纳维尔，斯托克斯方程，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程本质上是牛顿第三定律在流体中的表达，该定律指出，作用于物体的净力等于其质量与加速度的乘积，...。