纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组非线性偏微分方程，用于描述流体的运动，它由法国数学家克洛德，路易·纳维和爱尔兰物理学家乔治·加布里埃尔·斯托克斯于19世纪提出，纳维尔，斯托克斯方程可以描述各种流体，从可压缩气体到不可压缩液体，它们用于模拟天气预报、飞机设计和生物医学等领域中的流体行为，纳维尔，斯托克斯方程与牛顿运动定律纳...。

广义相对论预言了引力波的存在，但证实其存在并不容易，1916年，爱因斯坦在致史瓦西的信中提出了引力波的存在，将其比作电磁波在电磁场中的传播，他认为引力波以光速传播，并在源处释放能量，当时的数学处理并不完善，导致这些波的物理真实性受到质疑，特别是广义相对论具有坐标变换不变性，一些物理学家认为引力波可能只是坐标系的虚假现象，而非真实物理实...。

引言纳维尔，斯托克斯方程是流体力学中最重要的方程之一，描述了流体的运动，要了解这个方程，我们需要先了解张量语言，张量语言张量是数学中描述多维空间中量的一种工具，一阶张量就是矢量，二阶张量是矩阵，张量语言的好处是可以简化流体力学中的矢量计算，矢量微积分与张量语言矢量微积分是传统的流体力学工具，但张量语言可以简化其运算，例如，点乘可以用张...。

广义相对论预言了引力波的存在，但要证明其存在并不容易，1916年，爱因斯坦提出引力应具有波动，类似于电磁场中的电磁波，当时的数学处理不完善，使得这些波的物理实在性受到质疑，到1950年代，通过邦迪、皮拉尼和罗宾逊的努力，确定了引力波携带能量，邦迪在1957年通过Bondinews这一物理量，确切地描述了引力波如何从一个源中辐射出来，证...。

导言纳维尔，斯托克斯方程是描述流体运动的基本方程组，它以爱尔兰科学家乔治·加布里埃尔·斯托克斯爵士和法国数学家克劳德，路易·纳维的名字命名，是流体力学的基础，张量语言的简化力量传统的流体力学计算涉及大量的矢量计算，这些计算既复杂又容易出错，张量语言是一种强大的数学工具，它可以显著简化这些矢量计算，张量是具有多个分量的数学对象，它们可以...。

纳维尔，斯托克斯方程纳维尔，斯托克斯方程是一组微分方程，用于描述流体力学中流体的运动，它们以方程组的形式表达了牛顿第三运动定律，作用力等于反作用力，在流体中的应用，纳维尔，斯托克斯方程可以写成以下形式，$$\rho\frac，D\mathbf，u，Dt，=，\nablap，\mu\nabla^2\mathbf，u，$$其中，$\r...。

引力波的背景广义相对论的重要预言之一是引力波的存在，引力波是时空弯曲效应的传播，以光速传播，早在1916年，爱因斯坦就提出了引力波的概念，但其存在性直到多年后才得到证实，引力波的探测1974年，罗素·霍尔斯和约瑟夫·泰勒发现了第一颗脉冲双星系统PSRB1913，16，通过对该系统的观测，他们发现其轨道半长轴衰减与广义相对论预言的引力波...。

纳维尔，斯托克斯方程是流体力学中用来描述流体运动的基本方程，它以法国工程师克劳德，路易·纳维尔和爱尔兰数学家乔治·加布里埃尔·斯托克斯的名字命名，该方程是一个非线性偏微分方程组，用于描述流体的速度、压力和密度等物理量随时间和空间的变化，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程可以看作是牛顿运动定律在流体中的表达，牛顿运动...。

广义相对论预言了引力波的存在，但证实其存在并不容易，早在1916年，爱因斯坦就提出了引力可能存在波动，类似于电磁波在电磁场中的传播，爱因斯坦认为，引力波以光速传播，并从能量释放处释放能量，当时的数学处理不完善，导致这些波的物理真实性受到质疑，一些物理学家认为，引力波可能是坐标系的虚假现象，而不是真实物理实体，尽管存在这些质疑，物理学家...。

纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程，它是一个非线性偏微分方程组，如何理解这个方程组的物理意义，并将其与牛顿运动定律联系起来，是流体力学研究中的一个重要课题，张量语言在流体力学中的应用张量语言是一种数学工具，可以简化矢量微积分中的计算，在流体力学中，张量语言可以用来描述流体的运动、应力和应变，利用张量语言，我们可以将...。

引力波是广义相对论的重要预言，要证明其存在，需要找到能够传播能量的波动方程，早在1916年，爱因斯坦就提出应该存在引力的波动，类似于电磁波在电磁场中的传播，他认为引力波以光速传播，并在源处释放能量，当时的数学处理并不完善，使得这些波的物理实在性受到质疑，特别是广义相对论具有坐标变换不变的性质，一些物理学家认为引力波可能只是坐标系的虚假...。

如何表明广义相对论存在引力波，广义相对论是阿伯特·爱因斯坦于1915年提出的一个引力理论，它将引力视为时空弯曲的结果，而不是传统物理学中的吸引力，爱因斯坦预测广义相对论中存在引力波，类似于电磁波在电磁场中传播，证明引力波的存在并不容易，爱因斯坦对引力波的预测爱因斯坦最早在与瑞士物理学家卡尔·史瓦西的信件中提出引力波的存在，他认为引力波...。

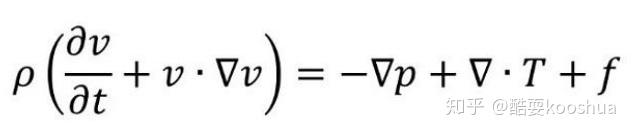
如何理解纳维尔，斯托克斯方程张量语言简介在流体力学中，矢量计算往往复杂繁琐，张量语言是一种简洁而有力的数学工具，可以极大地简化这些计算，在张量语言中，矢量被视为一阶张量，二阶张量则需要两个基底的张量积来展开，点乘和叉乘的张量表示矢量的点乘和叉乘可以通过张量进行表示，点乘，两个一阶矢量的缩并叉乘，一个一阶矢量与一个二阶张量的点乘，结果为...。

如何表明广义相对论存在引力波，广义相对论预言了引力波的存在，这是时空弯曲效应的传播，传播速度等于光速，根据广义相对论，引力波携带能量和动量，并从引力源，如黑洞合并或中子星碰撞，辐射出来，引力波的存在证明爱因斯坦在1916年首次提出引力波的存在，但直到20世纪后半叶才得到证实，以下是一些关键的步骤，1950年代，赫尔曼·邦迪等科学家确...。

回顾在上两节直播课中，张朝阳博士使用微分几何的语言计算了斯托克斯力，得到了斯托克斯力的形式，整个过程中仍然留有一个悬疑，即从微分几何的角度理解应力张量，本次直播课将彻底解决这一疑惑，单位基矢和坐标基矢回顾上节直播课的数学符号精神，在球坐标系下，单位基矢表示为，e，r=∂，∂re，θ=∂，∂θe，φ=∂，∂φ对这些单位基矢求偏导的结果可...。

纳维尔，斯托克斯方程是流体力学中的基本方程，描述了流体的运动，它是一个偏微分方程组，很难解析求解，张量语言的简化张量是描述物理量的数学工具，用张量语言可以简化流体力学中的矢量计算，使其更易于理解和推导，一阶和二阶张量矢量可以表示为一阶张量，用基底写成逆变形式，$$v^\alpha=，v^1，v^2，v^3，$$二阶张量需要用两个基底的...。

前言在流体力学中，纳维尔，斯托克斯方程是一组复杂的偏微分方程，描述流体的运动，它以克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯的名字命名，他们于19世纪制定了该方程，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程是牛顿第三运动定律在流体中的表达方式，它表示流体微元的受力等于作用在它上面的压力梯度和粘滞力，纳维尔，斯托克斯方...。

回顾微分几何求解非直角坐标系问题在之前的两节课中，我们用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，但在整个过程中，我们留有一个悬念，即从微分几何理解应力张量，本次讲座将彻底解决这一疑惑，微分几何的方式求解非直角坐标系问题非常方便，我们用球坐标系来做一个例子，在球坐标系下，单位基矢表示为，e，r=，sin，theta，c...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程是流体力学中描述流体运动的基本方程组，它是一个偏微分方程，将流体的质量、动量和能量联系起来，牛顿运动定律与纳维尔，斯托克斯方程的关联纳维尔，斯托克斯方程实际上是牛顿运动定律在流体中的表现形式，牛顿第三定律指出，作用力和反作用力大小相等，方向相反，这在流体力学中表现为，压强梯度力，流体中的压强...。

前言在，张朝阳的物理课，的直播课中，张朝阳博士使用微分几何的语言计算了斯托克斯力，本篇文章将彻底解决从微分几何理解应力张量的难题，回顾单位基矢和坐标基矢在球坐标系下，单位基矢为，$$，\bfe，\rho=\frac，\partial，\partial\rho，\quad，\bfe，\theta=\frac，1，\rho，\f...。

导言纳维尔，斯托克斯方程是描述流体运动的基本方程，它以数学形式表达了牛顿第二运动定律在流体中的应用，张量语言的引入张量语言是一种数学工具，可以简化流体动力学中的矢量计算，它允许我们用一个统一的符号表示点乘、叉乘和导数等运算，一阶张量又称矢量，可以用逆变形式表示为$V^，\alpha，$，其中$\alpha=1，2，3$是三个空间分量，...。

纳维尔，斯托克斯方程是流体力学中的基础方程，描述了流体的运动，它与牛顿运动定律有着密切的关系，可以通过牛顿第三定律导出，在传统的流体力学教材中，纳维尔，斯托克斯方程往往用矢量微积分的形式表示，这使得计算过程繁琐复杂，如果采用张量语言，纳维尔，斯托克斯方程的表达就会大大简化，张量语言是一种数学工具，它可以将矢量和二阶张量等物理量表示为坐...。

回顾，用微分几何求解非直角坐标系问题的便利性在之前的课程中，张朝阳介绍了使用微分几何来求解非直角坐标系问题的便利性，在球坐标系下，单位基矢和坐标基矢表示如下，单位基矢，$\hat，e，r=，\sin\theta\cos\phi，\sin\theta\sin\phi，\cos\theta，$，$\hat，e，\theta=，\cos...。

理解纳维尔，斯托克斯方程纳维尔，斯托克斯方程纳维尔，斯托克斯方程是流体动力学中的一组偏微分方程，描述了流体的运动，它由克劳德，路易·纳维尔和乔治·加布里埃尔·斯托克斯于19世纪开发，方程组如下，ρ，∂u，∂t，ρ，u·∇，u=，∇p，μ∇²u，μ，4，3，η，∇，∇·u，其中，ρ是流体的密度u是流体的速度p是流体中的压强μ是流体...。

回顾在，张朝阳的物理课，的第227期直播课程中，张朝阳博士回顾了利用微分几何求解非直角坐标系问题的便利性，并且说明了梯度项的数学内涵，应力张量概述斯托克斯定律描述了固体小球在流体中运动所受到的粘滞力，其中应力张量是关键，应力张量表示为，T=g[∇u，∇u，^T]，pI其中，g是度规u是速度矢量p是压力I是单位张量梯度项的数学表述梯度...。

2023年10月27日12时，，张朝阳的物理课，第二百二十八期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，首先回顾了如何用张量形式表达矢量微积分中的相关计算，再利用张量分析的方法从流体应力张量中导出了流体微元的受力，纳维尔，斯托克斯方程及其与牛顿运动定律的关联纳维尔，斯托克斯方程是流体力学中的基本方程之一...。

在之前的直播课程中，我们使用微分几何的语言计算了斯托克斯力，并得到了斯托克斯力的形式，从微分几何的角度理解应力张量仍然是一个悬而未决的问题，本次直播课程将彻底解决这一疑惑，非直角坐标系问题求解的便捷性回顾上一节直播课程，我们讲解了使用微分几何的方法求解非直角坐标系问题的便捷性，通过引入基矢和度规的概念，我们可以将几何问题转化为代数问题...。

引言纳维尔，斯托克斯方程是描述流体运动的数学方程组，对于了解流体力学至关重要，这些方程的复杂性可能令人望而生畏，本文将通过张量语言，简化流体力学中的矢量计算，从而帮助理解纳维尔，斯托克斯方程，纳维尔，斯托克斯方程与牛顿运动定律纳维尔，斯托克斯方程本质上是牛顿第三定律在流体中的表达，该定律指出，作用于物体的净力等于其质量与加速度的乘积，...。