微分几何推导斯托克斯定律并应用于粘滞阻力的应力张量

回顾：用微分几何求解非直角坐标系问题的便利性

在之前的课程中，张朝阳介绍了使用微分几何来求解非直角坐标系问题的便利性。在球坐标系下，单位基矢和坐标基矢表示如下：

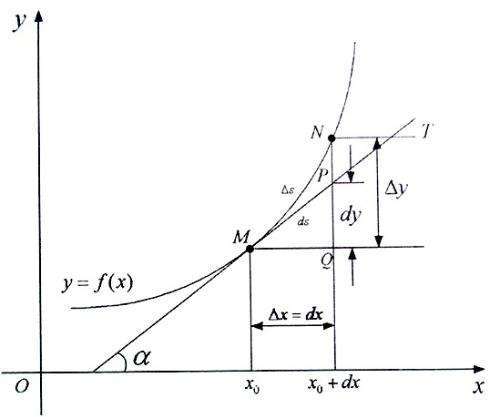
• 单位基矢：$\hat{e}_r = (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta)$, $\hat{e}_\theta = (\cos \theta \cos \phi, \cos \theta \sin \phi, -\sin \theta)$, $\hat{e}_\phi = (- \sin \phi, \cos \phi, 0)$

• 坐标基矢：$e_r = (\partial/\partial r)$, $e_\theta = (r^{-1} \partial/\partial \theta)$, $e_\phi = (r^{-1} \sin \theta \partial/\partial \phi)$

应力张量中梯度项的数学说明

斯托克斯定律描述了固体小球在流体中运动所受到的粘滞力。应力张量是斯托克斯力关键的物理量，其具体形式为： $$T^{ij} = \eta (\partial_i v_j + \partial_j v_i - \frac{2}{3} \delta_{ij} \partial_k v_k)$$ 其中，$\eta$是流体的粘度，$v$是速度矢量，$\partial_i$是协变导数，$\delta_{ij}$是克罗内克函数。

应力张量第二项的贡献

应力张量第二项的贡献可以写为： $$T^{21} = \eta \frac{\partial_1 v_2 + \partial_2 v_1}{g^{11}}$$ 其中，$g^{11}$是度规张量的逆。计算涉及克氏符和度规张量。

应力张量第三项的贡献

应力张量第三项的贡献可以写为： $$T^{31} = \eta \frac{\partial_3 v_1 + \partial_1 v_3}{g^{11}}$$ 计算过程与第二项类似。

结论

通过微分几何的语言，我们可以深入理解斯托克斯定律中应力张量的形式。梯度项的数学内涵以及应力张量各项对斯托克斯力的贡献过程都得到了清晰的阐述。