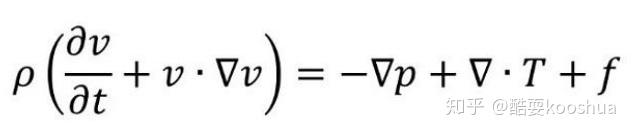
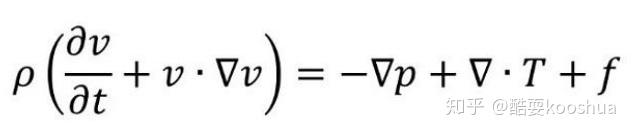如何理解纳维尔-斯托
克斯方程
张量语言简介
在
流体力学中，
矢量计算往往复杂繁琐。张量语言是一种简洁而有力的数学工具，可以极大地简化这些计算。在张量语言中，矢量被视为一阶张量，二阶张量则需要两个基底的张量积来展开。
点乘和叉乘的张量表示
矢量的点乘和叉乘可以通过张量进行表示：
点乘：两个一阶矢量的缩并
叉乘：一个一阶矢量与一个二阶张量的点乘，
结果为一阶矢量
梯度和散度的张量表示
矢量微积分中的
导数运算可以用张量语言表示：
梯度：一个函数（零阶张量）的协变导数，再升一次指标，得到逆变形式
散度：一个一阶矢量的协变导数，再缩并两个指标
纳维尔-
斯托克斯方程
纳维尔-斯托克斯方程描述了流体的运动，可以表示为：
ρ(∂u/∂t + u·∇u) = -∇p + μ∇²u
其中：
ρ 是流体的密度
u 是流体的速度矢量
t 是时间
p 是压强
μ 是流体的粘度
纳维尔-斯托克斯方程与牛顿第三定律
通过张量分析，可以从流体
应力张量中导出流体微元的受力，该受力正好对应纳维尔-斯托克斯方程中压强梯度项和粘滞项。这表明纳维尔-斯托克斯方程是牛顿第三定律在流体中的表达。
应用实例
导流定理
导流定理描述了不可压缩流体沿一条曲线的体积流量守恒，可以用张量语言表示为：
∇·u = 0
伯努利方程
伯努利方程描述了沿流线上的压强、速度和高度之间的关系，可以用张量语言表示为：
p + 1/2ρu² + ρgz = 常数
从张量语言推导纳维尔-斯托克斯方程
1. 流体应力张量
流体应力张量是一个二阶张量，描述了流体中各点之间的应力分布：
σ = -pδ + μ(∇u + (∇u)ᵀ)
其中：
p 是压强
δ 是单位张量
μ 是流体的粘度
(∇u)ᵀ 是速度梯度张量的转置
2. 流体微元受力
作用在流体微元上的受力为：
F = ∫∫σ·dA
其中：
F 是受力
σ 是应力张量
dA 是微元表面积
3. 导纳维尔-斯托克斯方程
利用高斯散度定理，
可以将受力表示为：
F = ∫∫∇·σ·dA = ∫V∇·σdV
其中：
∫V 是对流体微元体积的积分
再代入应力张量，并利用散度的张量表示，可以得到：
F = ∫V∇·(-pδ + μ(∇u + (∇u)ᵀ))dV
展开并化简，得到纳维尔-斯托克斯方程：
ρ(∂u/∂t + u·∇u) = -∇p + μ∇²u
总结
张量语言是一种简洁且有力的数学工具，可以极大地简化流体力学中的矢量计算。它不仅可以用来表达纳维尔-斯托克斯方程等复杂方程，还可以推导
其他重要的流体力学定理。
发表评论