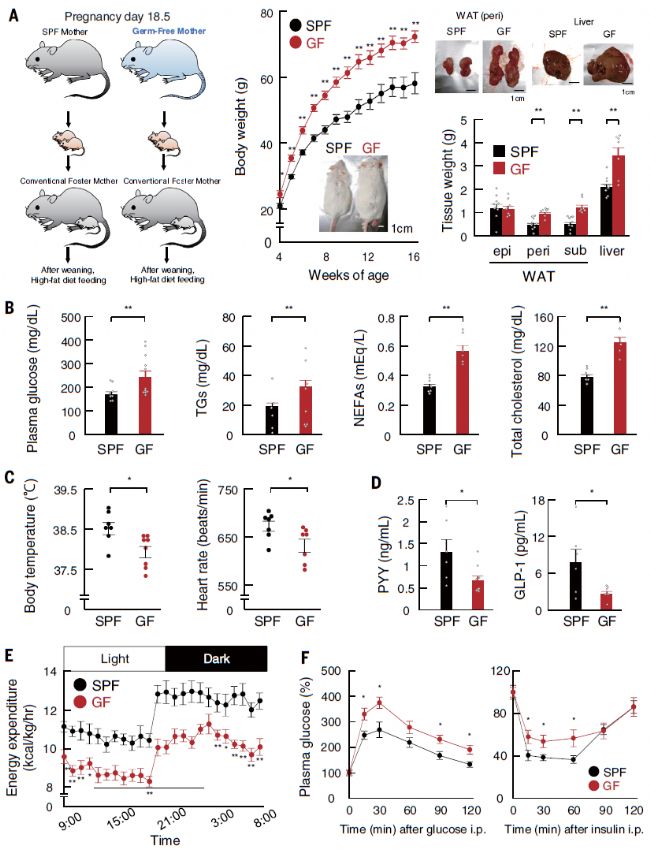
纳维尔-斯托克斯方程:使用张量语言简化流体力学
纳维尔-斯托克斯方程是什么?
纳维尔-斯托克斯方程是一组非线性偏微分方程,描述了流体的
运动。这些方程以 19
世纪物理学家纳维尔和斯托克斯的名字命名。
纳维尔-斯托克斯方程用于对不可压缩牛顿流体的流动进行建模。它们等效于牛顿第三定律(
作用力等于反作用力)在流体中的表达。
牛顿运动定律与纳维尔-斯托克斯方程
牛顿第三定律明确指出,作用在
物体上的力和对此物体产生的反作用力在大小和方向上相等且相反。在流体中,流体微元与周围流体相互作用。纳维尔-斯托克斯方程描述了流体微元上作用的所有力,包括压强梯度、粘性力、惯性力和重力。
张量语言简化
矢量计算
张量是描述物理量的一种数学工具,可以将矢量和二阶张量等不同类型的量统一起来。在流体力学中,使用张量可以大大简化矢量计算。
例如,在传统矢量微
积分中,矢量的点乘和叉乘运算需要特定的
规则。使用张量语言,这些运算可以表示为张量收缩,从而消除了对特殊规则的需要。
导数 u
Sando 张量语言
在矢量微积分中,Nabla 算符用于计算矢量的导数。Nabla 算符可以表示为协变导数,该导数考虑了坐标系的选取。
使用协变导数,可以将矢量的梯度、散度和旋度等运算表示为张量表达。这大大简化了这些运算,因为它们不再依赖于特定的坐标系。
纳维尔-斯托克斯方程的张量表达
使用张量语言,纳维尔-斯托克斯方程可以写成以下形式:
ρ(∂v/∂t) = -∇p + μ∇^2v + ρg
其中:
ρ 是流体的密度
v 是流体的速度
p 是流体的压强
μ 是流体的粘度
g 是重力加速度
结论
使用张量语言可以大大简化流体力学中的矢量计算。通过将矢量和二阶张量表示为张量,并使用协变导数来计算导数,可以消除对特殊规则和特定坐标系的依赖性。这种方法使得流体力学方程的推导和求解更加高效和简洁。


 纳维尔-斯托克斯方程:使用张量语言简化流体力学
纳维尔-斯托克斯方程是什么?
纳维尔-斯托克斯方程是一组非线性偏微分方程,描述了流体的运动。这些方程以 19 世纪物理学家纳维尔和斯托克斯的名字命名。
纳维尔-斯托克斯方程用于对不可压缩牛顿流体的流动进行建模。它们等效于牛顿第三定律(作用力等于反作用力)在流体中的表达。
牛顿运动定律与纳维尔-斯托克斯方程
牛顿第三定律明确指出,作用在物体上的力和对此物体产生的反作用力在大小和方向上相等且相反。在流体中,流体微元与周围流体相互作用。纳维尔-斯托克斯方程描述了流体微元上作用的所有力,包括压强梯度、粘性力、惯性力和重力。
张量语言简化矢量计算
张量是描述物理量的一种数学工具,可以将矢量和二阶张量等不同类型的量统一起来。在流体力学中,使用张量可以大大简化矢量计算。
例如,在传统矢量微积分中,矢量的点乘和叉乘运算需要特定的规则。使用张量语言,这些运算可以表示为张量收缩,从而消除了对特殊规则的需要。
导数 uSando 张量语言
在矢量微积分中,Nabla 算符用于计算矢量的导数。Nabla 算符可以表示为协变导数,该导数考虑了坐标系的选取。
使用协变导数,可以将矢量的梯度、散度和旋度等运算表示为张量表达。这大大简化了这些运算,因为它们不再依赖于特定的坐标系。
纳维尔-斯托克斯方程的张量表达
使用张量语言,纳维尔-斯托克斯方程可以写成以下形式:
ρ(∂v/∂t) = -∇p + μ∇^2v + ρg
其中:
ρ 是流体的密度
v 是流体的速度
p 是流体的压强
μ 是流体的粘度
g 是重力加速度
结论
使用张量语言可以大大简化流体力学中的矢量计算。通过将矢量和二阶张量表示为张量,并使用协变导数来计算导数,可以消除对特殊规则和特定坐标系的依赖性。这种方法使得流体力学方程的推导和求解更加高效和简洁。
纳维尔-斯托克斯方程:使用张量语言简化流体力学
纳维尔-斯托克斯方程是什么?
纳维尔-斯托克斯方程是一组非线性偏微分方程,描述了流体的运动。这些方程以 19 世纪物理学家纳维尔和斯托克斯的名字命名。
纳维尔-斯托克斯方程用于对不可压缩牛顿流体的流动进行建模。它们等效于牛顿第三定律(作用力等于反作用力)在流体中的表达。
牛顿运动定律与纳维尔-斯托克斯方程
牛顿第三定律明确指出,作用在物体上的力和对此物体产生的反作用力在大小和方向上相等且相反。在流体中,流体微元与周围流体相互作用。纳维尔-斯托克斯方程描述了流体微元上作用的所有力,包括压强梯度、粘性力、惯性力和重力。
张量语言简化矢量计算
张量是描述物理量的一种数学工具,可以将矢量和二阶张量等不同类型的量统一起来。在流体力学中,使用张量可以大大简化矢量计算。
例如,在传统矢量微积分中,矢量的点乘和叉乘运算需要特定的规则。使用张量语言,这些运算可以表示为张量收缩,从而消除了对特殊规则的需要。
导数 uSando 张量语言
在矢量微积分中,Nabla 算符用于计算矢量的导数。Nabla 算符可以表示为协变导数,该导数考虑了坐标系的选取。
使用协变导数,可以将矢量的梯度、散度和旋度等运算表示为张量表达。这大大简化了这些运算,因为它们不再依赖于特定的坐标系。
纳维尔-斯托克斯方程的张量表达
使用张量语言,纳维尔-斯托克斯方程可以写成以下形式:
ρ(∂v/∂t) = -∇p + μ∇^2v + ρg
其中:
ρ 是流体的密度
v 是流体的速度
p 是流体的压强
μ 是流体的粘度
g 是重力加速度
结论
使用张量语言可以大大简化流体力学中的矢量计算。通过将矢量和二阶张量表示为张量,并使用协变导数来计算导数,可以消除对特殊规则和特定坐标系的依赖性。这种方法使得流体力学方程的推导和求解更加高效和简洁。








发表评论