探索广义相对论中的线性引力波 张朝阳的物理课 揭开宇宙的和声

引力波是广义相对论的重要预言。1916年，爱因斯坦在致史瓦西的信中首次提出引力波的存在。他认为引力波以光速传播，并带有能量。但当时数学处理不完备，导致这些波的物理真实性受到质疑。有些物理学家认为引力波可能是坐标系虚假变化的结果，而非真实物理实体。

20世纪50年代，邦迪、皮拉尼和罗宾逊确定了引力波携带能量。邦迪在1957年通过邦迪新闻参数明确描述了引力波如何从源中辐射出来，证明了引力波可以在不依赖坐标系的情况下携带能量、动量和角动量。

考虑弱场下的平直时空微扰。时空度规可以展开为背景时空度规加上微扰。

$$\tilde{g}_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}$$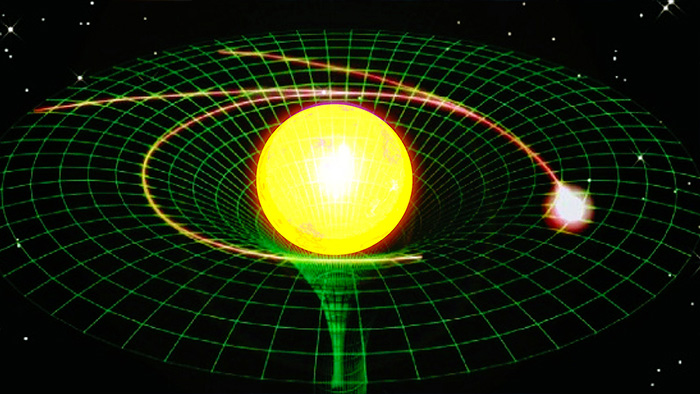

其中$\eta_{\mu\nu}$是平直时空度规，$h_{\mu\nu}$是微扰。将度规代入爱因斯坦方程，展开并取线性项，得到引力微扰的波动方程：

$$\Box h_{\mu\nu} = \frac{1}{2} \partial_\mu \partial_\nu h^\alpha_\alpha - \partial_\alpha \partial_\beta h_\mu^\beta - \partial_\alpha \partial_\beta h_\nu^\beta + \partial^\alpha \partial^\beta (h_{\alpha\beta} - \frac{1}{2} \eta_{\alpha\beta} h^\gamma_\gamma)$$

其中$\Box$是达朗贝尔算子，定义为$\Box = \partial_\mu \partial^\mu$。这个波动方程描述了引力波在时空中的传播。

引力波是广义相对论的重要预言。通过对脉冲双星系统的观测和LIGO的探测，已经充分证明了引力波的存在。引力微扰的波动方程描述了引力波在时空中的传播。这些发现为研究宇宙提供了重要的工具，开启了引力波天文学的新时代。