张朝阳的物理课揭示广义相对论下的线性引力波 透过宇宙的声音

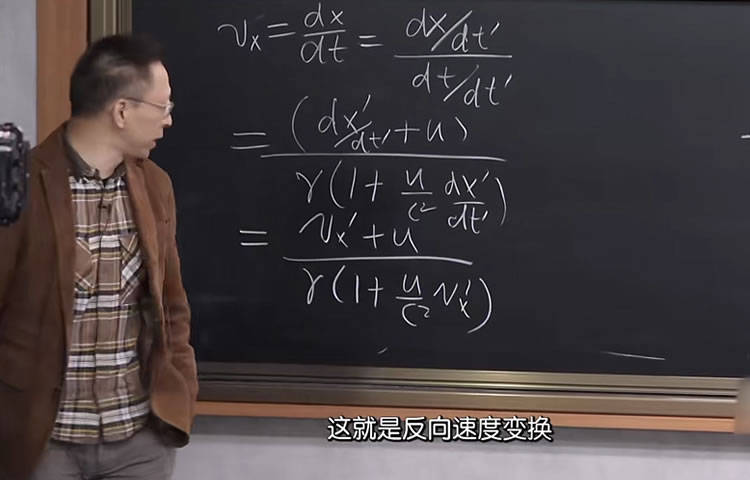
引力波：广义相对论的预言

广义相对论预测引力波的存在，这是时空曲率效应的传播。引力波以光速传播，并从源处释放能量。

早在1916年，爱因斯坦就提出了引力波的概念，但由于当时的数学处理不完善，引力波的物理实在性受到质疑。一些物理学家认为引力波可能是坐标系的虚假现象，而非真实物理实体。

引力波的理论确认

尽管存在质疑，物理学家们仍继续研究广义相对论和引力波的数学基础。到1950年代，赫尔曼·邦迪、费利克斯·皮拉尼和伊凡·罗宾逊确定了引力波携带能量。

1962年，雷纳·萨克斯和约瑟夫·波多尔斯基提出了萨克斯-戈德堡公式，进一步规范了描述引力波的方法。至此，人们已确信广义相对论中存在引力波。

引力波的间接证据

1974年，罗素·霍尔斯和约瑟夫·泰勒发现了第一颗脉冲双星系统PSRB1913+16。通过对该系统的长期观测，他们发现其轨道半长轴衰减与广义相对论预言的引力波耗散一致。

这一发现间接证明了引力波的存在，也为霍尔斯和泰勒赢得了1993年诺贝尔物理学奖。

引力波探测

1969年，约瑟夫·韦伯设计并建造了韦伯棒用于探测引力波。虽然他声称探测到了引力波，但其结果后来被认为是噪声干扰。

1990年代，激光干涉引力波天文台（LIGO）项目启动。2015年，LIGO探测器成功探测到了首个引力波事件GW150914，这是两个黑洞合并产生的引力波。这一事件验证了爱因斯坦的广义相对论，开启了引力波天文学的新时代。

引力微扰的波动方程

在广义相对论的弱场情形下，爱因斯坦方程可以化简为波动方程。张朝阳演示了这一理论推导的过程：

时空微扰度规

对时空做微扰展开，背景时空为平直时空，微扰项用小写希腊字母表示：

g = η + h

弱场下的爱因斯坦方程

弱场条件下，的爱因斯坦方程可以化简为：

□h = -16πG T 其中： □是达朗贝尔算子 G是万有引力常数 T 是应力-能量张量

波动方程

对弱场下的爱因斯坦方程两边分别取迹，得：

∂ ∂ h = 0

对弱场下的爱因斯坦方程取迹并减去波方程，得：

∂ ∂ h = -16πG T 其中T是應力-能量張量的迹。

合并以上两个方程，即可得到引力微扰的波动方程：

□h - 1/2η ∂ ∂ h = -16πG T

这表明，引力微扰满足波动方程，并可以传播于时空之中。

总结

引力波是广义相对论的重要预言，其存在性已通过理论推导和间接观测得到确认。LIGO的探测直接验证了引力波的存在，开启了引力波天文学的新时代。

在弱场情形下，引力微扰满足波动方程，这表明引力波可以传播于时空之中。上述理论推导过程展示了广义相对论的数学力量，以及其对宇宙现象的深刻洞察。